Leecode 0572. Subtree of Another Tree

572. Subtree of Another Tree

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

Example 1:

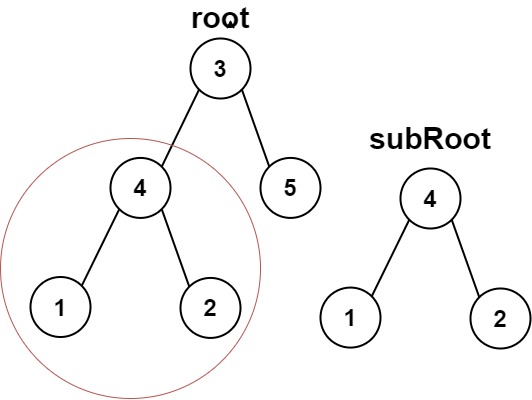
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true

Example 2:

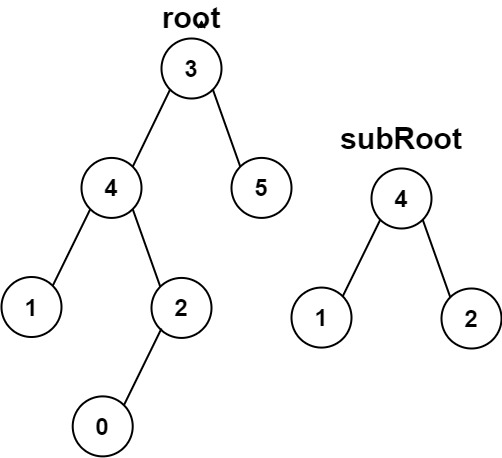
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false

题目大意

给定两棵二叉树的根节点 root 和 subRoot，判断 subRoot 是否是 root 的子树。子树的定义是：root 中存在一个节点，该节点及其所有后代组成的树与 subRoot 结构完全相同、节点值完全一致（root 本身也可视为自身的子树）。

例如：

• 输入 root = [3,4,5,1,2]、subRoot = [4,1,2]，root 中节点 4 及其后代（1、2）与 subRoot 完全一致，返回 true；
• 输入 root = [3,4,5,1,2,null,null,null,null,0]、subRoot = [4,1,2]，root 中节点 4 的后代多了节点 0，与 subRoot 不同，返回 false。

解题思路

判断子树的核心是两步验证：

1. 判断当前节点是否匹配：检查以 root 中某个节点为根的子树，是否与 subRoot 完全相同（复用「100. 相同的树」的逻辑）；
2. 遍历所有可能的节点：若当前节点不匹配，则递归检查 root 的左子树和右子树，直到找到匹配的子树或遍历完所有节点。

具体步骤：

1. 若 subRoot 为空，直接返回 true（空树是任何树的子树）；
2. 若 root 为空但 subRoot 非空，返回 false（非空树不能是空地的子树）；
3. 检查当前 root 与 subRoot 是否相同，若相同返回 true；
4. 若当前节点不匹配，递归检查 root 的左子树和右子树是否包含 subRoot。

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    // 计算二叉树高度（同104. 二叉树的最大深度）
    int getHeight(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        int left_h = getHeight(root->left);
        int right_h = getHeight(root->right);
        return max(left_h, right_h) + 1;
    }

    // 判断两棵树是否相同（同100. 相同的树）
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr || q == nullptr) {
            return p == q; // 只有两者都为nullptr时才返回true
        }
        return p->val == q->val &&
               isSameTree(p->left, q->left) &&
               isSameTree(p->right, q->right);
    }

public:
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        // 计算subRoot的高度，作为后续判断的筛选条件
        int hs = getHeight(subRoot);

        // 递归lambda表达式：返回当前节点的高度和是否找到匹配的子树
        auto dfs = [&](this auto&& dfs, TreeNode* node) -> pair<int, bool> {
            if (node == nullptr) {
                return {0, false}; // 空节点高度为0，未找到匹配
            }
            
            // 递归处理左右子树
            auto [left_h, left_found] = dfs(node->left);
            auto [right_h, right_found] = dfs(node->right);
            
            // 如果左子树或右子树已经找到匹配的子树，直接返回true
            if (left_found || right_found) {
                return {0, true};
            }
            
            // 计算当前节点的高度
            int node_h = max(left_h, right_h) + 1;
            
            // 只有当当前节点高度等于subRoot高度时，才检查是否为相同的树
            return {node_h, node_h == hs && isSameTree(node, subRoot)};
        };
        
        // 从根节点开始DFS，返回是否找到子树
        return dfs(root).second;
    }
};