199. Binary Tree Right Side View

Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.

Example 1:

Input: root = [1,2,3,null,5,null,4]

Output: [1,3,4]

Explanation:

img

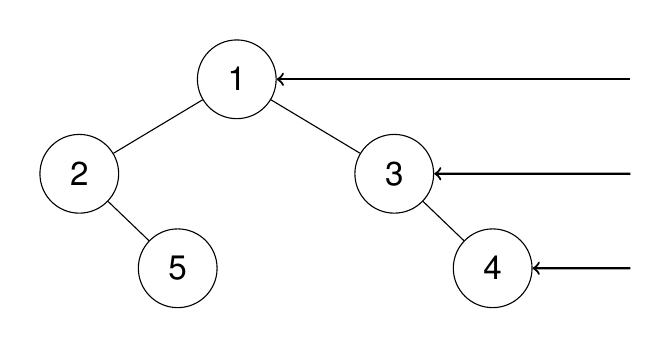
Example 2:

Input: root = [1,2,3,4,null,null,null,5]

Output: [1,3,4,5]

Explanation:

img

Example 3:

Input: root = [1,null,3]

Output: [1,3]

Example 4:

Input: root = []

Output: []

题目大意

给定一棵二叉树的根节点 root，想象自己站在树的右侧，返回从顶部到底部能看到的节点值。核心是：每一层只保留「最右侧」的一个节点值，按层从上到下排列。

例如：

  • 输入二叉树 [1,2,3,null,5,null,4]，右视图为 [1,3,4]（第一层最右是 1，第二层最右是 3，第三层最右是 4）。

解题思路

这种实现的核心思想是利用深度优先搜索（DFS），但改变了访问顺序：

  1. 先递归访问右子树，再递归访问左子树
  2. 记录当前遍历的深度，当某个深度是第一次到达时，当前节点就是该深度从右侧能看到的节点
  3. 用结果数组的大小来跟踪已经记录的深度，当深度等于结果数组大小时，说明是首次到达该深度

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> result;
        // 从根节点开始，初始深度为0
        dfs(root, 0, result);
        return result;
    }
    
private:
    // 深度优先搜索：先右后左
    void dfs(TreeNode* node, int depth, vector<int>& result) {
        if (node == nullptr) return;
        
        // 关键：当当前深度等于结果集大小，说明是首次到达该深度
        // 此时的节点就是该深度从右侧能看到的节点
        if (depth == result.size()) {
            result.push_back(node->val);
        }
        
        // 先递归右子树，再递归左子树
        dfs(node->right, depth + 1, result);
        dfs(node->left, depth + 1, result);
    }
};