637. Average of Levels in Binary Tree

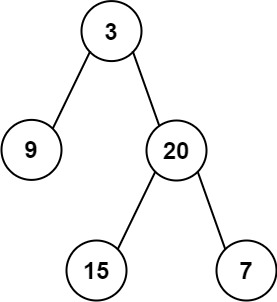
Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted.

Example 1:

img

1
2
3
4
Input: root = [3,9,20,null,null,15,7]
Output: [3.00000,14.50000,11.00000]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return [3, 14.5, 11].

Example 2:

img

1
2
Input: root = [3,9,20,15,7]
Output: [3.00000,14.50000,11.00000]

题目大意

给定一棵二叉树的根节点 root，返回二叉树每一层节点值的平均值，结果以数组形式呈现（允许与实际答案的误差在 10⁻⁵ 以内）。

例如：

  • 输入二叉树 [3,9,20,null,null,15,7]，第一层（根节点）平均值为 3.0，第二层（9、20）平均值为 14.5，第三层（15、7）平均值为 11.0，最终返回 [3.0, 14.5, 11.0]。

解题思路

层平均值的核心是按层统计节点值的总和与个数，因此仍基于「层序遍历（BFS）」实现，步骤如下：

  1. 层序遍历初始化：若根节点为空，直接返回空数组；否则将根节点入队。

  2. 逐层处理节点：

    • 记录当前队列大小（即当前层的节点总数 levelSize），用于后续计算平均值。

    • 初始化当前层的「值总和sum」，遍历当前层的所有节点：

      • 取出队首节点，将其值累加到 sum。
      • 依次将节点的左、右子节点入队（为下一层遍历做准备）。

    • 计算当前层的平均值（sum / levelSize，注意用浮点数计算），加入结果集。

  3. 遍历结束：所有层处理完成后，返回结果集。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        vector<double> result;
        if (root == nullptr) { // 边界条件：空树返回空数组
            return result;
        }

        queue<TreeNode*> q;
        q.push(root); // 根节点入队，启动层序遍历

        while (!q.empty()) {
            int levelSize = q.size(); // 当前层的节点总数
            double levelSum = 0.0;    // 当前层的节点值总和（用double避免整数溢出）

            // 遍历当前层的所有节点
            for (int i = 0; i < levelSize; ++i) {
                TreeNode* curr = q.front();
                q.pop();

                levelSum += curr->val; // 累加当前节点值

                // 下一层节点入队（左子节点先入，右子节点后入，不影响统计）
                if (curr->left != nullptr) {
                    q.push(curr->left);
                }
                if (curr->right != nullptr) {
                    q.push(curr->right);
                }
            }

            // 计算当前层平均值，加入结果集
            double avg = levelSum / levelSize;
            result.push_back(avg);
        }

        return result;
    }
};